Half life::
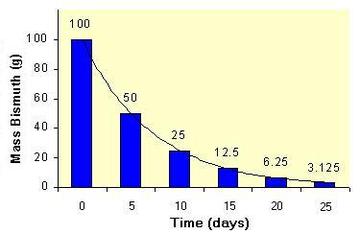
A half-life often described to the decay of discrete entities, such as radioactive atoms. In that container, it does not work to use the definition "Half-life is the time required for accurately half of the entities to decay". For example, if there is one radioactive atom with a half-life of one second, there will not be "half of an atom" left after one second. There will be either one atom left or zero atom left, depending on whether or not the atom happens to decay.
Formula for Half Life Time: A more spontaneous characteristic of exponential decay is the time required to decay to half of its initial quantity by the decaying quantity. This time is known as half-life; it can be denoted by the symbol t1 / 2. The half-life can also be written in terms of the decay constant, or the mean lifetime, as
t1/2 =ln 2 /λ = τ ln 2
Because, 1/λ = τ
When the Half life expression can be inserted for τ in the exponential equation above, and ln2 is engaged into the base, this equation can be written as
N(t) = N0 2-t / t1/2
Where,
N0 - the first quantity of the thing that will decay
t1 / 2 - Half life
τ - Mean lifetime of the decaying quantity,
λ - Decay constant of the decaying quantity
Thus, the quantity of material left is 2 − 1 = 1 / 2 raised to the (whole or fractional) number of half-lives that have alreadypassed. Thus, after three half-lives there will be 1 / 23 = 1 / 8 of the unique material left.
So, the mean lifetime τ is directly proportional to the half life. The mathematical expression of mean life time is
τ = t1/2 / ln 2
= 1.442695040888963. t1/2
Having problem with formula for Strain keep reading my upcoming posts, i will try to help you.
Example
Suppose there is a radioactive substance having a half-life of 10 minutes. If in the begining we have a 500 g sample, how much of the original amount will remains after one hour?
Explanation
The easiest way to attack these questions is to start with the original amount of the sample, then draw arrows representing each half-life. One hour is 60 minutes, so that’s six half-lives. At the end of the given time period, 7.8 g remains.
500 g250 g125 g62.5 g31.25 g15.625 g7.8125 g
Applications Exponential decay occurs in a wide selection of situations. Most of these decrease into the domain of the natural sciences. Any submission of mathematics to the social sciences or humanities is uncertain, because of the strange complexity of human behavior. However, a few generally exponential phenomena have been identified there as well.
Many decay processes that are frequently treated as exponential, are really only exponential so long as the model is large and the law of large numbers holds. For small samples, a more general study is necessary, accounting for a Poisson process.
Formula for Half Life Time: A more spontaneous characteristic of exponential decay is the time required to decay to half of its initial quantity by the decaying quantity. This time is known as half-life; it can be denoted by the symbol t1 / 2. The half-life can also be written in terms of the decay constant, or the mean lifetime, as
t1/2 =ln 2 /λ = τ ln 2
Because, 1/λ = τ
When the Half life expression can be inserted for τ in the exponential equation above, and ln2 is engaged into the base, this equation can be written as
N(t) = N0 2-t / t1/2
Where,
N0 - the first quantity of the thing that will decay
t1 / 2 - Half life
τ - Mean lifetime of the decaying quantity,
λ - Decay constant of the decaying quantity
Thus, the quantity of material left is 2 − 1 = 1 / 2 raised to the (whole or fractional) number of half-lives that have alreadypassed. Thus, after three half-lives there will be 1 / 23 = 1 / 8 of the unique material left.
So, the mean lifetime τ is directly proportional to the half life. The mathematical expression of mean life time is
τ = t1/2 / ln 2
= 1.442695040888963. t1/2
Having problem with formula for Strain keep reading my upcoming posts, i will try to help you.
Example
Suppose there is a radioactive substance having a half-life of 10 minutes. If in the begining we have a 500 g sample, how much of the original amount will remains after one hour?
Explanation
The easiest way to attack these questions is to start with the original amount of the sample, then draw arrows representing each half-life. One hour is 60 minutes, so that’s six half-lives. At the end of the given time period, 7.8 g remains.
500 g250 g125 g62.5 g31.25 g15.625 g7.8125 g
Applications Exponential decay occurs in a wide selection of situations. Most of these decrease into the domain of the natural sciences. Any submission of mathematics to the social sciences or humanities is uncertain, because of the strange complexity of human behavior. However, a few generally exponential phenomena have been identified there as well.
Many decay processes that are frequently treated as exponential, are really only exponential so long as the model is large and the law of large numbers holds. For small samples, a more general study is necessary, accounting for a Poisson process.
